Question

An element with mass 730 grams decays by 27.6% per minute. How much of the element is remaining after 12 minutes, to the nearest 10th of a gram?

Answer 1

Here you go

Look at the image

Answer 2

Answer: 15.1 gram

Explanation:

The exponential decay equation with rate of decay r in time period t is given by :-

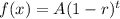`f(x)=A(1-r)^t`, A is the initial value .

Given: The initial mass of element= 730 grams

Rate of decay= 27.6%=0.276

Thus, the function represents the amount of element after t minutes is given by ;-

`f(x)=730(1-0.276)^x\\\\\Rightarrow\ f(x)=730(0.724)^x`

Now, the function represents the amount of element after 12 minutes is given by ;-

`f(x)=730(0.724)^(12)\\\\\Rightarrow\ f(x)=15.1420841187\approx15.1\text{ grams}`

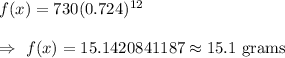
Hence, 15.1 grams of element remains after 12 minutes.