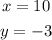Question

Find the values of x and y.The angle on the left (5x-17)°

Answer 1

You need to remember that:

- A Straight Angle is an angle that measures 180 degrees.

- Supplementary Angles are those angles that add up to 180 degrees.

- Vertical Angles are those pairs of opposite angles that share the same vertex. They are congruent.

Then, knowing these definitions, you can identify that these pair of angles are Vertical Angles:

`\begin{gathered} \mleft(5x-17\mright)\degree\text{ } \\ \\ \mleft(3x+3\mright)\degree \end{gathered}`

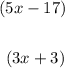
Therefore, you can set up the following equation (because they are congruent):

`5x-17=3x+3`

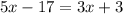
Now you need to solve for "x" in order to find its value:

`\begin{gathered} 5x-17-3x=3 \\ 2x=3+17 \\ 2x=20 \\ \\ x=(20)/(2) \\ \\ x=10 \end{gathered}`

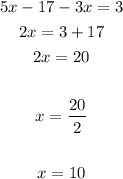
Notice that these angles are Supplementary Angles:

`\begin{gathered} (3x+3)\degree \\ \\ (9x-19y)\degree \end{gathered}`

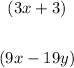
Then, you can set up this equation:

`(3x+3)+(9x-19y)=180`

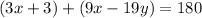
Knowing the value of "x", you can substitute it into the equation and solve for "y":

`\begin{gathered} (3)(10)+3+(9)(10)-19y=180 \\ 30+3+90-19y=180 \\ 123-19y=180 \\ -19y=180-123 \\ -19y=57 \\ \\ y=(57)/(-19) \\ \\ y=-3 \end{gathered}`

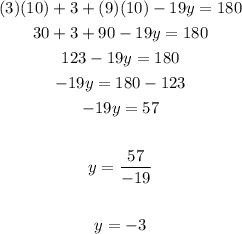
Then, the answer is:

`\begin{gathered} x=10 \\ y=-3 \end{gathered}`