Question

A circle is centered at the point (-3, 2) and passes through the point (1, 5). The radius of the circle is ? units. The point (-7, ? ) lies on this circle.

Answer 1

The circle has like equation: (x+3)²+(y-2)²=r²

If x=1 then y=5 ==>(1+3)²+(5-2)²=r²==>4²+3²=r²==>r=5 (the radius)

if x=-7 then (-7+3)²+(y-2)²=25 ==> (y-2)²=25-16==>y=2+3 or y=2-3
The points (-7,5) and (-7,-1) are on the circle.

Enjoy :D

Answer 2

radius of the circle is 5 units.

the circle passes through the points (-7,5) and (-7, -1).

Explanation:

The center of the circle is (-3, 2) and it passes through (1,5)

The standard form of a circle is given by

`(x-h)^2+(y-k)^2=r^2`

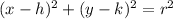
Here, we have

h = -3, k = 2, x= 1, y = 5

Plugging these values, we get

`(1+3)^2+(5-2)^2=r^2\\\\r^2=4^2+3^2\\\\r^2=16+9\\\\r^2=25\\\\r-=5`

Therefore, the radius of the circle is 5 units.

Now, we have been given that

x = -7 and we have to find the value of y.

The equation of circle is

`(x+3)^2+(y-2)^2=5^2`

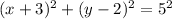
Plugging, x = -7 and find y

`(-7+3)^2+(y-2)^2=25\\\\16+(y-2)^2=25\\\\(y-2)^2=9\\\\y-2=\pm3\\\\y=3+2,y=-3+2\\\\y=5,-1`

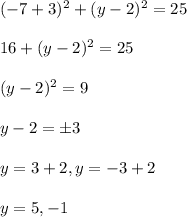
Therefore, the circle passes through the points (-7,5) and (-7, -1).