Answer: x = ± i , x = ±√2i are solution .
Explanation:
Given :
 , use u substitution to solve.
, use u substitution to solve.
To find : what are the solutions of the equation .
Solution : We have given that
 .
.
Let consider
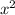 = u .
= u .
Substitute u =
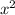 in given equation .
in given equation .
 .
.
On factoring
 .
.
Taking common
u( u+2) +1 (u+2) = 0.
On grouping
(u+1) (u+2) =0
Now, u+1 = 0 ⇒ u = -1.
u+2 = 0 ⇒ u = -2.
In term of x, plugging
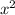 = u.
= u.
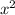 = -1 ;
= -1 ;
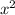 = -2.
= -2.
taking square root both side
x = ± i
x = ±√2i.
Therefore, x = ± i , x = ±√2i are solution .