The total angles in a triangle are 180degrees.
Therefore,
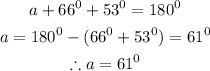
In order to solve for the distances of the other two sides, we will use the Sine rule formula.
which says,
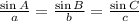
Where,
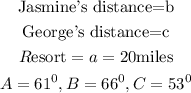
Solving for George's distance (c)

Solving for Jasmine distance (b)
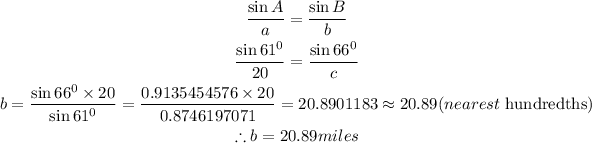
Hence,
Jasmine will drive 20.89miles to arrive at the resort.
George will drive 18.26miles to arrive at the resort.