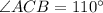Question

The perpendicular bisectors of sides AC and BC of ΔABC intersect side AB at points P and Q respectively, and intersect each other in the exterior (outside) of ΔABC. Find the measure of ∠ACB if m∠CPQ = 78° and m∠CQP = 62°.

Answer 1

I took the test today follow the picture I've displayed

Answer 2

Answer:
`\angle ACB=110^(\circ)`

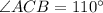
Explanation:

Here, The perpendicular bisectors of sides AC and BC of ΔABC intersect side AB at points P and Q respectively, and intersect each other in the exterior (outside) of
`\triangle ABC`

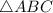
Let L is the mid point of side BC while M is the mid point of side AC.(mentioned on below figure).

Then, In triangles QBL and QLC,

QL=QL, ( reflexive)

BL=LC, ( by the property of mid points)

And,
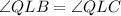`\angle QLB= \angle QLC` ( right angles)

Therefore
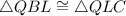`\triangle QBL\cong \triangle QLC`, (SAS)

Thus,
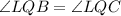`\angle LQB=\angle LQC` ( by CPCT)

But,
`\angle LQB+\angle LQC+\angle CQP = 180^(\circ)`

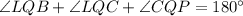
Thus,
`\angle LQB=59^(\circ)`

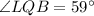
Now, In
`\triangle QBL`,

`\angle QBL+\angle BLQ+\angle LQB=180^(\circ)`

⇒
`\angle QBL=31^(\circ)`=
`\angle ABC`

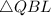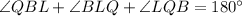
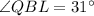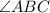
Similarly,
`\triangle PMC\cong \triangle PMA`

Then
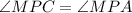`\angle MPC=\angle MPA` ( by CPCT)

But,
`\angle CPQ+\angle MPC+\angle MPA = 180^(\circ)`

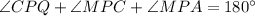
Thus,
`\angle MPA=51^(\circ)`

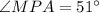
Now, In
`\triangle MPA`,

`\angle MPA+\angle PAM+\angle AMP=180^(\circ)`

⇒
`\angle MAP=39^(\circ)`=
`\angle BAC`

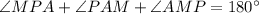
Again, In
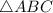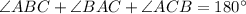
`\triangle ABC`,

`\angle ABC+ \angle BAC+\angle ACB = 180^(\circ)`

`31^(\circ)+39^(\circ)+\angle ACB = 180^(\circ)`

⇒
`\angle ACB=110^(\circ)`