The given function is,
![f(x)=-\sqrt[]{x-2}\text{ , x>2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6nzyv0unvg12lre3l9xh.png)
Steps to find the inverse:
Step 1
Replace f(x) with y.
![y=-\sqrt[]{x-2}\text{ }](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wxnyqd6xhp3l8yoqx5oc.png)
Step 2
Replace x with y and y with x in equation from step 1.
![x=-\sqrt[]{y-2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5a4cv61fpvx116ffyhsr.png)
Step 3
Solve the equation from step 2 for y.
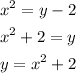
Step 4
Replace y with f^-1(x).
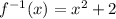
Therefore, the inverse of f(x) is ,
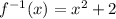
The inverse function f(x) is in the shape of a parabola opening upwards.
The graph of inverse function is,
If a vertical line drawn does not intersect tha graph more than once, then the graph is of a function(vertical line test).
Since a vertical line does not intersect the graph more than once, the inverse of f(x) is a function.
Since the inverse of f(x) is defined at all points in the interval (-∞, ∞), the domain of the inverse of f(x) is (-∞, ∞).
The range of the inverse of f(x) is [2,∞)