Question

Use f(x) = 4x – 2 and g(x) = 5 – x^2 to evaluate the expression.(a)(f o g)(-2)(b)(g o f)(-2)

Answer 1

Given the functions:

`\begin{gathered} f(x)=4x-2 \\ g(x)=5-x^2 \end{gathered}`

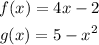
We will find (f o g)(-2)

So, first, we will find the function (f o g)(x) as follows:

`\begin{gathered} \mleft(f\circ g\mright)(x)=f\lbrack g(x)\rbrack=4(5-x^2)-2 \\ (f\circ g)(x)=20-4x^2-2 \\ (f\circ g)(x)=18-4x^2 \end{gathered}`

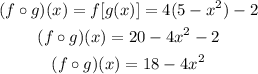
Now, substitute with x = -2

so,

`(f\circ g)(-2)=18-4\cdot(-2)^2=18-4\cdot4=18-16=2`

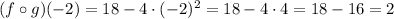
so, the answer to the part (a) (f o g)(-2) = 2

b) (g o f)(-2)

We will find (g o f)(x) as follows:

`(g\circ f)(x)=g\lbrack f(x)\rbrack=5-(4x-2)^2`

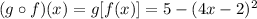
Substitute with x = -2

So,

`\begin{gathered} (g\circ f)(-2)=5-(4\cdot-2-2)^2 \\ =5-(-8-2)^2 \\ =5-(-10)^2 \\ =5-100 \\ =-95 \end{gathered}`

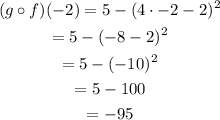
So, the answer to the part (b): (g o f)(-2) = -95