Given the function
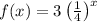
When x = -2
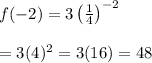
Thus, (-2, 48) lies on the graph of the given function.
When x = 0
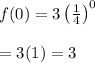
Thus, (0, 3) lies on the graph of the given function.
When x = 2
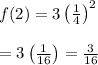
Thus, (2, 3/16) lies on the graph of the given function.
When x = 12
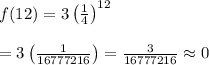
Thus, (12, 0) lies on the graph of the given function.