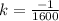Answer:
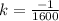
Explanation:
Given data:
half life of radium is 1600 year
the equation is given as
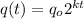
As it is given, quantity is going halved, thus k is is going to be -ve. thus equation become

we know that
 ....1
....1
as it is half life so we have
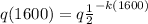 ......2
......2
comparn 1 and 2 we get
1 = - k(1600)