Question

Which of the following represents the zeros of f(x) = 2x3 − 5x2 − 28x + 15?

5, −3, −1 over 2
5, −3, 1 over 2
5, 3, −1 over 2
5, 3, 1 over 2

Answer 1

It is 5, -3,
`(1)/(2)`
So B
I just took the test and got it correct!

Answer 2

Answer: B) 5, −3, 1 over 2 are the zeros of f(x).

Explanation:

Given function f(x)=
`2x^3-5x^2-28x+15`

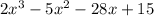
If a is a zero of f(x) then f(a)=0

Let's check all the options

`f(5)=2(5)^3-5(5)^2-28(5)+15\\=2(125)-5(25)-28(5)+15=250-125-140+15=0`

`f(-3)=2(-3)^3-5(-3)^2-28(-3)+15\\=2(-27)-5(9)-28(-3)+15=-54-45+84+15=0`

`f((-1)/(2))=2(-1)/(2)()^3-5((-1)/(2))^2-28((-1)/(2))+15\\=2((-1)/(8))-5((-1)/(4))+14+15=(-1)/(4)-(5)/(4)+29=(110)/(4)=(55)/(2)\\eq 0`

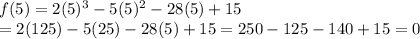
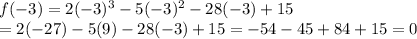
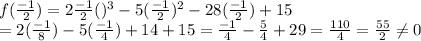
Therefore , 5 and -3 are zeroes of f(x).but -1/2 is not.

`f((1)/(2))=2(1)/(2)()^3-5((1)/(2))^2-28((1)/(2))+15\\=2((1)/(8))-5((1)/(4))-14+15=(1)/(4)-(5)/(4)-14+15=0`

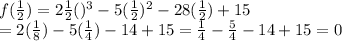
⇒ 1/2 isthe third zero of f(x).

Here we got our three zeroes as 5,-3,1/2,rest other will not satisfy f(a)=0

Therefore B represents the zeroes of f(x).