Step-by-step explanation
The distance traveled by a particle with velocity v(t) in the interval [3,13] is given by the following integral:
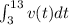
However, we can't calculate this integral since we don't have the equation of v(t). What we do have is a table with the value of v for several t's. We can use the values in this table to approximate the integral I wrote above with a trapezoidal sum.
For the function v(t) we have:
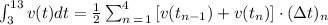
Where the t's with subindices are the t values given by the table:
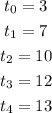
And the Δt's are the lengths of the intervals defined by two consecutive t's. Let's find each Δt:
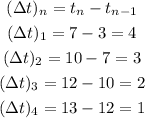
Now I'm going to write the full expression of the trapezoidal sum (expanding the sum):
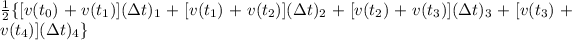
Now we use the corresponding v(t) values from the table and we obtain:

Answer
Then the answer is the third option, 115.50.