Question

Find tanθ exactly if sinθ=-9/41, and θ is in the fourth quadrant

Answer 1

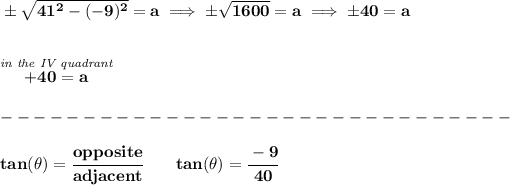
keep in mind that, in the IV quadrant, sine or the y-coordinate is negative, and the cosine or x-coordinate is positive, whilst the hypotenuse or radius, is just a distance unit and is never negative.

now, we know the angle is in the IV quadrant, therefore the opposite side or "y" is negative, thus


`\bf sin(\theta )=-\cfrac{9}{41}\implies sin(\theta )=\cfrac{\stackrel{opposite}{-9}}{\stackrel{hypotenuse}{41}} \\\\\\ \textit{so, now let's find the \underline{adjacent side} then} \\\\\\ \textit{using the pythagorean theorem}\\\\ c^2=a^2+b^2\implies \pm√(c^2-b^2)=a\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases}`


`\bf \pm√(41^2-(-9)^2)=a\implies \pm√(1600)=a\implies \pm 40=a \\\\\\ \stackrel{\textit{in the IV quadrant}}{+40=a}\\\\ -------------------------------\\\\ tan(\theta)=\cfrac{opposite}{adjacent}\qquad tan(\theta)=\cfrac{-9}{40}`