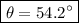Question

Solve for the indicated angle to the nearest tenth of a degree.
o
18
25

Answer 1

`\theta=54.2^\circ`

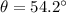
Explanation:

Right Triangles

The ratios of the sides of a right triangle are called trigonometric ratios. Each acute angle has an adjacent side and an opposite side. The trigonometric ratios are defined upon those sides.

The tangent ratio is defined as:

`\displaystyle \tan\theta=\frac{\text{opposite side}}{\text{adjacent side}}`

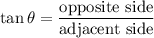
The opposite side is 25 and the adjacent side is 18, thus:

`\displaystyle \tan\theta=(25)/(18)=1.389`

The angle is calculated by using the inverse tangent function:

`\theta=\arctan 1.389`

`\boxed{\theta=54.2^\circ}`