Question

Which of there polynomials could have (x-2) as a factor?

a(x) = 6x² - 7x - 5

b(x) = 3x² + 15x - 42

c(x) = 2x³ + 13x² + 16x + 5

d(x) = 3x³ - 2x² - 15x + 14

e(x) = 8x⁴ - 41x³ - 18x² + 101x + 70

f(x) = x⁴ + 5x³ - 27x² - 101x - 70

Answer 1

x-2 is a factor of following polynomials:

• b(x) = 3x² + 15x - 42
• d(x) = 3x³ - 2x² - 15x + 14
• e(x) = 8x⁴ - 41x³ - 18x² + 101x + 70

Explanation:

In order to check that which polynomials might have x-2 as a factor, we will put

x-2 = 0 => x = 2 in each polynomial, if the value of polynomial on 2 is zero then x-2 is a factor otherwise not.

So,

a(x) = 6x² - 7x - 5

Putting x = 2

`a(2) = 6(2)^2-7(2)-5\\= 6(4)-14-5\\=24-14-5\\=24-19\\=5 \\eq 0`

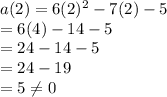
b(x) = 3x² + 15x - 42

`b(2) = 3(2)^2 + 15(2) - 42\\=3(4)+30-42\\=12+30-42\\=42-42 = 0`

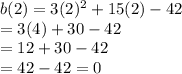
c(x) = 2x³ + 13x² + 16x + 5

`c(2) = 2(2)^3 + 13(2)^2 + 16(2) + 5\\=2(8)+13(4)+32+5\\=16+52+32+5\\=105 \\eq 0`

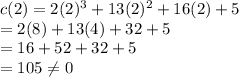
d(x) = 3x³ - 2x² - 15x + 14

`d(2) = 3(2)^3 - 2(2)^2 - 15(2) + 14\\= 3(8)-2(4)-30+14\\=24-8-30+14\\=38-38 = 0`

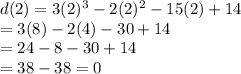
e(x) = 8x⁴ - 41x³ - 18x² + 101x + 70

`e(2) = 8(2)^4 - 41(2)^3 - 18(2)^2 + 101(2) + 70\\= 8(16)-41(8)-18(4)+202+70\\=128-328-72+202+70\\=0`

`f(2) = (2)^4 + 5(2)^3 - 27(2)^2 - 101(2) - 70\\=16+5(8)-27(4)-202-70\\=16+40-108-202-70\\=-324 \\eq 0`

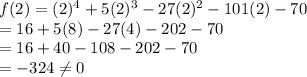
Hence,

x-2 is a factor of following polynomials:

• b(x) = 3x² + 15x - 42
• d(x) = 3x³ - 2x² - 15x + 14
• e(x) = 8x⁴ - 41x³ - 18x² + 101x + 70