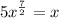1 Answer

Mehdi Mohammadpour · Answer 1 · 2022-03-16T02:18:18+0000

Answer:

The log equation is given such as

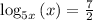
$\log _(5x)\left(x\right)=(7)/(2)$

The log equation as an exponential equation is:

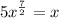
$\:5x^{(7)/(2)}=x$

Explanation:

Given

The log equation is given such as

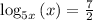
$\log _(5x)\left(x\right)=(7)/(2)$

To determine

Write the log equation as an exponential equation.

Given the log equation

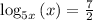
$\log _(5x)\left(x\right)=(7)/(2)$

Apply the logarithmic definition.

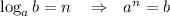
$\log _ab=n\:\:\:\:\Rightarrow \:\:\:a^n=b$

Thus,

$\:5x^{(7)/(2)}=x$

Please log in or register to add a comment.