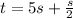Answer:
The correct answer is: Option D:
Explanation:
Given that
Weight of snail is s
We have to use the given statements to write the mathematical expression
The snail drank water 5 times of its weight
So the quantity of water will be 5s
And it ate half of its weight's food which will be s/2
The combined weight of water and food will be:
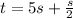
Hence,
The correct answer is: Option D: