Question

What is the approximate length of the midsegment parallel to BC. the coordinates are B(-6,1) C(5,-1) ? please help

Answer 1

I think it would be around 5 1/2 approximately

Answer 2

Explanation:

Let the mid-point of BC is M. So, the length of BM = MC.

The coordinates of B are (-6, 1) and coordinates of C are (5, -1). Therefore, using the distance formula find the distance as follows.

d =
`\sqrt{(x_(2)-x_(1))^(2) + (y_(2)-y_(1))^(2)}`

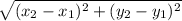
Place the values form points B and C into the above formula as follows.

d =
`\sqrt{(x_(2)-x_(1))^(2) + (y_(2)-y_(1))^(2)}`

=
`\sqrt{(5- (-6))^(2) + ((-1)- (1))^(2)}`

=
`\sqrt{(11)^(2) + (-2)^(2)}`

=
`√(121 + 4)`

=
`√(125)`

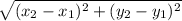
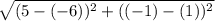
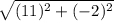
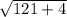
= 11.18 (approx)

Therefore, the length of mid-point of line segment will be
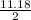`(11.18)/(2)` = 5.59 (approx). BM = MC = 5.59.

The length of line segment which is parallel to BC =
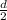`(d)/(2)`.