Answer:
The inverse of function
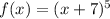 is
is
![\mathbf{f^(-1) (x)=\sqrt[5]{x}+7}](https://img.qammunity.org/2022/formulas/mathematics/college/3esrath9pye54ggtbsy3fuoo34eoap13em.png)
Option A is correct option.
Explanation:
For the function
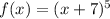 , Find
, Find
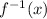
For finding inverse of x,
First let:
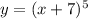
Now replace x with y and y with x
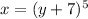
Now, solve for y
Taking 5th square root on both sides
![\sqrt[5]{x}=\sqrt[5]{(y+7)^5}\\\sqrt[5]{x}=y+7\\=> y+7=\sqrt[5]{x}\\y=\sqrt[5]{x}-7](https://img.qammunity.org/2022/formulas/mathematics/college/4sq3bs1v3zqvrozjgmu6vwqjf5jjcnlz5m.png)
Now, replace y with
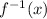
![f^(-1) (x)=\sqrt[5]{x}+7](https://img.qammunity.org/2022/formulas/mathematics/college/r76tobni7904avc2vzegiu78tlbi53ot4h.png)
So, the inverse of function
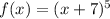 is
is
![\mathbf{f^(-1) (x)=\sqrt[5]{x}+7}](https://img.qammunity.org/2022/formulas/mathematics/college/3esrath9pye54ggtbsy3fuoo34eoap13em.png)
Option A is correct option.