Question

49x2 - 81 is an example of the difference of two

squares. All polynomials that are a difference of two
squares factor in a very specific way. Which of the
following would represent the factorization of a polynomial
that was the difference of two squares.
(x - 25)
(9x – 100)
(25x – 4)(25x – 4)
(x-4) (x-9)
(4x + 3)(4x - 3)

Answer 1

(4x + 3)(4x - 3) represents the factorization of a polynomial that was the difference of two squares as it is written as product of sum and difference of two numbers.

Explanation:

Formulas are used to factorize the polynomials.

In the given question, we can see a difference of squares

the difference of squares can be factorized using the formula

`a^2-b^2 = (a+b)(a-b)`

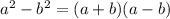
Here a^2 and b^2 are squares and factorized as sum and difference of numbers.

So in the given options,

(4x + 3)(4x - 3) represents the factorization of a polynomial that was the difference of two squares as it is written as product of sum and difference of two numbers.