Answer:
The correct option is 4.
Explanation:
Given information:
Bring lunch : 46 males, 254 females
Buy lunch : 176 males, 264 females
Total number of peoples is
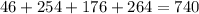
Total number of males is
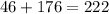
The probability of male is
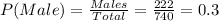
Since probability of males is 0.3, therefore options A and C are incorrect.
Total number of persons who buys lunch is
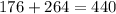
The probability of persons who buys lunch is

We need to find the probability of P(male | buys lunch).
According to the conditional probability, we get
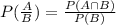
P(male | buys lunch)
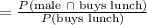
P(male | buys lunch)
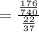
P(male | buys lunch)
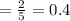
Therefore the correct option is 4.