Answer:
1) AB=7 CD=3 EF=
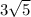 2)
2)
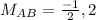
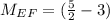 \\
\\
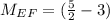 3) AB not inclined CD not inclined EF 6/5
3) AB not inclined CD not inclined EF 6/5
Explanation:
1) We can use the Distance Formula to answer the 1st. question.
But in the first case AB I'd rather doing it intuitively because it is a straight line parallel to the x-axis
AB
A(-4,2) and B(3,2)
In this segment, also parallel we can calculate the length as |-4|+|3|=7 since both have the same y coordinate.
Using the Distance formula to check it:
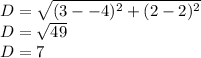
CD
C(-4,-1) D(-4,-4)
Similar to the first one but this time with different y coordinates.
The length will be calculated by subtracting the absolute values for y:
|-4|-|-1|=4-1 = 3
Using the Distance formula to check it:
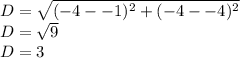
EF
E (1,-1) F(4,-5)
In this case there's no straight line.
So right to the Distance Formula:

2) To find the Midpoints we need to calculate the Mean of these two points.
AB
A(-4,2) and B(3,2)
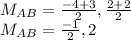
CD
C(-4,-1) D(-4,-4)

EF
E (1,-1) F(4,-5)
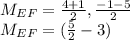
3) To find the Slope let's calculate the quotient of a difference between y-coordinates over x-coordinates of two given points.
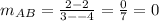
AB is not inclined.
CD
C(-4,-1) D(-4,-4)
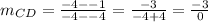
Not Defined for all Real Set of Numbers
The line CD is not inclined.
EF
E(1,-1) F(4,-5)
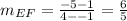
The line EF has a slope of 6/5