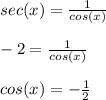
If you know your sine/cosine values you know that when:
cos(x) = 1/2 , sin(x) = √(3)/2
The fact that theta, or "x" as I've been using... terminates in Quadrant III means both cosine and sine will be negative and then cotangent will be positive.
cot(x) = cos(x) / sin(x)
cot(x) = (-1/2) / (-√(3)/2)
cot(x) = (1/2) * (2/√(3))
cot(x) = 1/√(3)
or rationalized as √(3)/3