What is the measure of angle ACB?

Question

asked Jul 4, 2018 13.1k views

2 Answers

Vadim Khotilovich · Answer 1 · 2018-07-07T19:27:50+0000

Answer:

The correct option is B.

Explanation:

From the given graph it is clear that the measure of arc AB is 100°.

Let the center of circle of the circle be O.

According to the central angle theorem, the angled inscribed on a circle is half of its central angle.

Using central angle theorem,

$\angle ABX=(1)/(2)* \angle AOX$

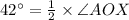
$42^(\circ)=(1)/(2)* \angle AOX$

Multiply 2 on both the sides.

$42^(\circ)* 2=\angle AOX$

$84^(\circ)=\angle AOX$

The central angle of arc AX is 84°. So the measure of arc AX is 84°.

Using tangent secant theorem,

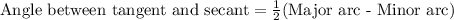
$\text{Angle between tangent and secant}=(1)/(2)(\text{Major arc - Minor arc})$

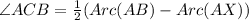
$\angle ACB=(1)/(2)(Arc(AB)-Arc(AX))$

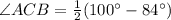
$\angle ACB=(1)/(2)(100^(\circ)-84^(\circ))$

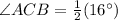
$\angle ACB=(1)/(2)(16^(\circ))$

$\angle ACB=8^(\circ)$

Therefore the measure of angle ACB is 8° Therefore the correct option is B.