Question

Given the function h(x) = 4x, Section A is from x = 0 to x = 1 and Section B is from x = 2 to x = 3.

Part A: Find the average rate of change of each section. (4 points)

Part B: How many times greater is the average rate of change of Section B than Section A? Explain why one rate of change is greater than the other. (6 points)

Answer 1

Average rate of change in Section A:


`(h(1)-h(0))/(1-0)=(4-0)/(1-0)=4`

Average rate of change in Section B:


`(h(3)-h(2))/(3-2)=(12-8)/(3-2)=4`

As you can see, the average rates of change are the same, as expected.
`h(x)=4x` is linear, which means it has a constant rate of change over any interval in its domain.

Answer 2

The rate of change of section A is 3 and rate of change of section B is 48.

Explanation:

The given function is

`h(x)=4^x`

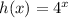
Formula for average rate:

`m=(f(x_2)-f(x_1))/(x_2-x_1)`

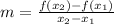
Section A is from x = 0 to x = 1, the average rate of change of section A is

`m_1=(h(1)-h(0))/(1-0)=(4-1)/(1)=3`

Section B is from x = 2 to x = 3, the average rate of change of section B is

`m_2=(h(3)-h(2))/(3-2)=(64-16)/(1)=48`

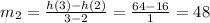
Therefore rate of change of section A is 3 and rate of change of section B is 48.

`m_1* k=m_2`

`3* k=48`

`k=12`

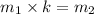
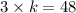
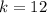
Therefore average rate of change of Section B is 12 times of Section A.

The given function is an exponential function and rate of change is not constant.