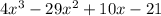Question

If s(x)=x-7 and t(x)=4x^2-x+3 , which expression is equivalent to (t*s)(x)

Answer 1

that equation is equivalent to 4(x - 7)^2 - (x - 7) + 3

Answer 2

The answer is
`4x^3-29x^2+10x-21`

Explanation:

In order to determine the answer, we have to know what it means (t*s)(x).

When we need to multiply two functions, where y(x) and z(x) are the functions, we can describe the process with the notation (y*z) (x). This notation means that the function y(x) is being multiplying by the function z(x).

So, in this case, we have two functions:

`s(x)=x-7\\t(x)=4x^2-x+3`

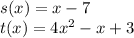
Multiplying both functions (t*s) (x):

`(t*s)(x)=t(x)*s(x)\\(4x^2-x+3)(x-7)\\4x^3-28x^2-x^2+7x+3x-21\\4x^3-29x^2+10x-21`

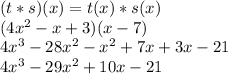
Finally, the expression is:

`4x^3-29x^2+10x-21`