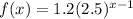Question

Which formula can be used to describe the sequence? 1.2, 3, 7.5, 18, 7.5, ...

Answer 1

Option A)
`1.2(2.5)^(x-1)`

Explanation:

We are given a series:

`1.2, 3, 7.5, 18.75, ...`

We know that the given series is a geometric series as

`\displaystyle(3)/(1.2) = (7.5)/(3) = (18.75)/(7.5) = 2.5`

Geometric Series:

• A geometric series is a series with a constant ratio between successive terms.
• The first term is represented by a
• In the given series a = 1.2
• The common ratio is denoted by r
• For the given series r = 2.5

The
`n^(th)` term of a geometric series is given by:

`a_n = a(r)^(n-1)`

`a_1= 1.2\\a_2 = 1.2(2.5)^(2-1) = 3\\a_3 = 1.2(2.5)^(3-1) = 7.5\\a_4 = 1.2(2.5)^(4-1) = 18.75`

Thus, the general term of the given series can be formulated with the help of
`f(x) = 1.2(2.5)^(x-1)`

Option A)
`1.2(2.5)^(x-1)`

Answer 2

The given sequence is 1.2, 3, 7.5, 18.75, ...,
This is a geometric sequence with common ratio of 2.5, because
3/1.2 = 2.5
7.5/3 = 2.5
18.75/7.5 = 2.5

The 1st term is a₁ = 1.2(2.5)⁰
The 2nd term is a₂ = 1.2(2.5)¹
The 3rd term is a₃ = 1.2(2.5)²
and so on

Therefore the sequence obeys the formula
f(x) = 1.2(2.5)ˣ⁻¹

Answer:
`f(x) = 1.2(2.5)^(x-1)`