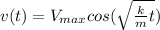Question

The maximum speed of a mass m on an oscillating spring is vmax . what is the speed of the mass at the instant when the kinetic and potential energy are equal?

Answer 1

Let
A = the amplitude of vibration
k = the spring constant
m = the mass of the object

The displacement at time, t, is of the form
x(t) = A cos(ωt)
where
ω = the circular frequency.

The velocity is
v(t) = -ωA sin(ωt)

The maximum velocity occurs when the sin function is either 1 or -1.
Therefore

`v_(max) = \omega A`
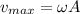
Therefore

`v(t) = -V_(max) sin(\omega t)`

The KE (kinetic energy) is given by

`KE = (m)/(2)v^(2) = (m)/(2) V_(max)^(2) sin^(2) (\omega t)`

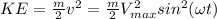
The PE (potential energy) is given by

`PE = (k)/(2) x^(2) = (k)/(2) A^(2) cos^(2) (\omega t)`

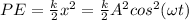
When the KE and PE are equal, then

`v^(2) = (k)/(m) A^(2) cos^(2) (\omega t)`

For the oscillating spring,

`\omega ^(2) = (k)/(m) \\ V_(max) = \omega A = \sqrt{ (k)/(m) } A`
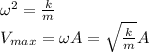
Therefore

`v^(2) = (k)/(m) (m)/(k) V_(max)^(2) cos^(2) ( \sqrt{ (k)/(m) t} ) \\ v = V_(max) \,cos( \sqrt{ (k)/(m) t} )`

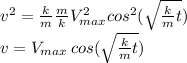
Answer:
`v(t) = V_(max) cos( \sqrt{ (k)/(m) t} )`