Question

Unfortunately, arsenic occurs naturally in some ground water†. a mean arsenic level of μ = 8.0 parts per billion (ppb) is considered safe for agricultural use. a well in texas is used to water cotton crops. this well is tested on a regular basis for arsenic. a random sample of 36 tests gave a sample mean of x = 6.8 ppb arsenic, with s = 2.9 ppb. does this information indicate that the mean level of arsenic in this well is less than 8 ppb? use α = 0.01. (a) what is the level of significance? 0.01 state the null and alternate hypotheses. h0: μ = 8 ppb; h1: μ > 8 ppb h0: μ = 8 ppb; h1: μ < 8 ppb h0: μ > 8 ppb; h1: μ = 8 ppb h0: μ < 8 ppb; h1: μ = 8 ppb h0: μ = 8 ppb; h1: μ ≠ 8 ppb (b) what sampling distribution will you use? explain the rationale for your choice of sampling distribution. the standard normal, since the sample size is large and σ is known. the student's t, since the sample size is large and σ is unknown. the student's t, since the sample size is large and σ is known. the standard normal, since the sample size is large and σ is unknown. what is the value of the sample test statistic? (round your answer to three decimal places.) -2.483 (c) estimate the p-value. p-value > 0.250 0.125 < p-value < 0.250 0.050 < p-value < 0.125 0.025 < p-value < 0.050 0.005 < p-value < 0.025 p-value < 0.005 sketch the sampling distribution and show the area corresponding to the p-value. webassign plot webassign plot webassign plot webassign plot (d) based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis? are the data statistically significant at level α? at the α = 0.01 level, we reject the null hypothesis and conclude the data are statistically significant. at the α = 0.01 level, we reject the null hypothesis and conclude the data are not statistically significant. at the α = 0.01 level, we fail to reject the null hypothesis and conclude the data are statistically significant. at the α = 0.01 level, we fail to reject the null hypothesis and conclude the data are not statistically significant. (e) interpret your conclusion in the context of the application. there is sufficient evidence at the 0.01 level to conclude that the mean level of arsenic in the well is less than 8 ppb. there is insufficient evidence at the 0.01 level to conclude that the mean level of arsenic in the well is less than 8 ppb.

Answer 1

Part A:

For a hypothesis test, the significant level is given by α. From the question, we were told that α = 0.01.

Therefore, the significant level is 0.01.

Our previous knowledge is that a mean arsenic level of μ = 8.0 parts per billion (ppb) is considered safe for agricultural use, we know want to know from a sample of 36 tests whether the mean level of arsenic in a particular well is less than 8 ppb.

Therefore, the null and the alternative hypothesis are:


`H_0:\mu=8\ pbb \\ \\ H_a:\mu\ \textless \ 8\ pbb`



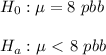
Part B:

The sampling distribution to be used is the student's t, since the sample size is large and σ is unknown.

The test statistics is given by:


`t= \frac{\bar{x}-\mu}{s/√(n)} \\ \\ = (6.8-8)/(2.9/√(36)) \\ \\ = (-1.2)/(2.9/6) = (-1.2)/(0.4833) \\ \\ =-2.483`



Part C:

The p-value for a t-distribution test statistics of -2.483 with a degree of freedom of 35 is given by 0.0090

Thus 0.005 < p-value < 0.025



Part D:

Since the p-value is less that the significant level, we reject the null hypothesis and conclude the data are statistically significant.

i.e.
at the α = 0.01 level, we reject the null hypothesis and conclude the data are statistically significant.



Part E:

Therefore, we conclude that there is sufficient evidence at the 0.01 level to conclude that the mean level of arsenic in the well is less than 8 ppb.