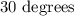We will investigate how to determine an angle formed by a straight line relative to any horizontal line plot on a two dimensional cartesian coordinate grid.
The following two equation of lines are given:
![\begin{gathered} y\text{ = }\frac{\sqrt[]{3}}{3}\cdot x\text{ + }2\text{ }\ldots Eq1 \\ \\ y\text{ = 2 }\ldots\text{ Eq2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wkm6alzfmrni0sxrm3yg.png)
All straight lines are expressed in the standard general form of an equation of a line:
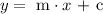
Where,
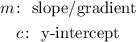
To determine an angle we must always deal with the reference equation of a line. The reference equation of a line is a horizontal line parallel to the ( x-axis ). So the anlge formed between the (Eq1) and (Eq2) is equivalent to the angle formed between (Eq1) and the x-axis.
To determine the angle of any line with respect to the x-axis. We seek help from trigonometric ratios. There are three type of trigonometric ratios as follows:
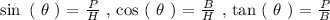
Where,

For sine and cosine trigonometric ratio we will need to evaluate the length of the line ( H ). This can be a tedious process. However, for the case of tangent ratio we need the sides ( P and B ).
The sides ( P ) and ( B ) can be denoted as ( rise ) and ( run ) of the straight line. The ratio of rise over run is also expressed by the parameter of the equation of straight line as follows:

The above relation always holds true for ALL straight lines!
We can therefore modify our tangent ratio as such:
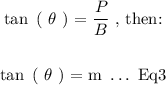
The (Eq3) is almost always used to determine the angle between any line (Eq1) and any horizontal line like ( Eq2 ). Its a standard result!
We will use the ( Eq3 ) to determine the angle formed as follows:
![\tan (\theta)\text{ = }\frac{\sqrt[]{3}}{3},\text{ ( m ) taken from Eq1}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9pdaaxkg9uveutjt9g8o.png)
Next we recall the standard angle table for all trigonometric ratios as shown below:
From the above table we can see the value of angle denoted in the top row and the corresponding ratios for each trigonometric function.
Locate the tan ( theta ) row-4,column-1. Then locate the trigonometric ratio Column-3!
Then read out the angle at Row-1 and column-3. The angle defined is:
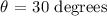
Hence, the angle between the given two lines is: