Answer:
Perpendicular
Explanation:
General equation of line:
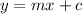
Line 1: 6x+10y=20
Convert in general equation
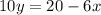
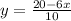
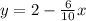

Line 2: 5x-3y=21
Convert in general equation
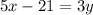
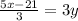

if slopes are equal then the lines are parallel
If the product of slopes is -1 then they are perpendicular
Since
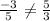
So, lines are not parallel

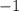
Since the product of slopes is -1
Hence the given lines are perpendicular