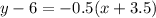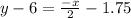Question

how to figure out the equation of the perpendicular bisector of a line when the end points of the line are given?

Answer 1

First find the equation of the line, Ill use the first one as an example:

(-5,10) , ( -9,2)

To work out the gradient:

`(y_2 - y_1)/(x_2 - x_1)`

`(2 - 10)/(-9 - -5) = (-8)/(-4) = 2`

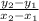
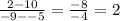
So the gradient of the line is 2

The midpoint of the line is
`( (-5 + -9)/(2), (10+2)/(2)) = ( -3.5, 6)`
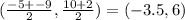
The gradient of the inverted line is -0.5 as it is the negative reciprocal of the gradient of the first line.
Here, we work out the equation of the bisector.

`y-6 = -0.5(x+3.5)`

`y-6 = (-x)/(2)-1.75`

`y = -(1)/(2) x+4.25`