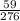Question

7. In a survey, 156 people indicated that they prefer cats, 59 indicated that they prefer dogs, and 61 indicated that they don't enjoy either pet. Find the probability that a randomly chosen person will prefer dogs.

Answer 1

Let C and D be the set of people who prefer cats and dogs respectively.

According to the given problem,

`\begin{gathered} n(C)=156 \\ n(D)=59 \\ n(none)=61 \end{gathered}`

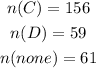
Note that mathematically, you can prefer one thing at a time. That means that none of the surveyed people will prefer cat and dog both,

`n(C\cap D)=0`

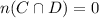
Then the total number of people surveyed is calculated as,

`\begin{gathered} n(Total)=n(C)+n(D)+n(none) \\ n(Total)=156+59+61 \\ n(Total)=276 \end{gathered}`

The probability of an event is given by,

`\text{ Probability}=\frac{\text{ Number of favorable outcomes}}{\text{ Total number of outcomes}}`

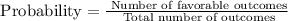
So the probability that a randomly chosen person will prefer dogs, is calculated as,

`\begin{gathered} P(D)=(n(D))/(n(Total)) \\ P(D)=(59)/(276) \end{gathered}`

Thus, the corresponding probability is,

`(59)/(276)`