Question

What point do all graphs of the form y=a^x where ≠ 0 have in common?

A.(0, 1)
B.(1, 0)
C.(1, 1)
D.(0, 0)

Answer 1

answer is A.(0, 1)
because
when x = 0, y=a^0 = 1
so (0,1)

hope it helps

Answer 2

A.(0, 1)

Explanation:

This is an exponential function, which is a function where the independent variable x appears in the exponent and has a constant a as its base. Its mathematical expression is:

`f(x)=a^x\\\\\{x\in R: (a\\eq0\hspace{3}and\hspace{3}x\in Z)or(a\geq0\hspace{3}and\hspace{3}x>0)or(x\geq 1 \hspace{3}and\hspace{3}x\in Z)or\hspace{3}a>0\}`

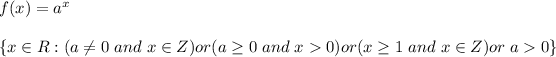
The image of 0 is always 1 and the image of 1 is always a:

`f(0)=a^0=1\\f(1)=a^1=a`

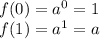
Thus, exponential functions always pass through the points (0, 1) and (1, a).

I attached you a graph that illustrates the behavior of the function.