Question

What is the solution of x2+x-6/x-7<0

Answer 1

The solution of the expression lies in
`(-\infty,-3)\cup (2,7)`

Explanation:

Given : Expression
`(x^2+x-6)/(x-7)<0`

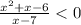
To find : What is the solution of teh expression ?

Solution :

Expression
`(x^2+x-6)/(x-7)<0`

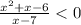
First we factor the numerator,

`((x-2)(x+3))/(x-7)<0`

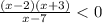
The solution is by putting numerator equal to zero.

(x-2)(x+3)=0

(x-2)=0 , (x+3)=0

x=2 , x=-3

The solution is by putting denominator equal to zero.

(x-7)=0

x=7

As at x=7 the function is not defined.

The domain for the above inequality is
`(-\infty,7)\cup (7,\infty)`

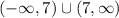
For each root we create a test,

For x<-3 it is true.

For -3<x<2 it is not true.

For
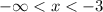`-\infty<x<-3` it is true.

For 2<x<7 it is true.

The solution of the expression lies in
`(-\infty,-3)\cup (2,7)`