The Solution.
The probability that an experiment involve yawning is given as below:
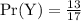
The probability that an experiment does not involve yawning is
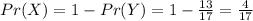
By Binomial expansion, we have that

So, the probability that exactly 11 out of the randomly chosen 14 experiments involve yawning is

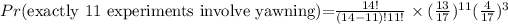
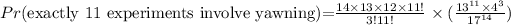

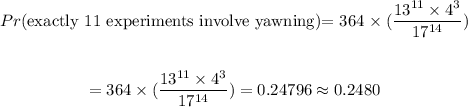
Thus, the correct answer is 0.2480