Question

The volume of a sphere is 1/48 PI cubic meters. What is the length of the sphere’s radius? In your final answer, include all of your calculations. (ALL CALCULATIONS PLEASE )

Answer 1

Volume of sphere = 4/3 πr^3
Volume = 1/48π
1/48 = 4/3 πr^3

0.02083 = 1.3 x 3.14 x r^3
r^3 = 0.02083/1.3 x 3.14
r^3 = 0.00693
r = 0.19 meters

Answer 2

`r=(1)/(4)\text{ m}=0.25\text{ m}`

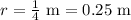
Explanation:

We have been given that volume of a sphere is
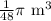`(1)/(48)\pi\text{ m}^3`. We are asked to find the length of sphere's radius.

To find the radius of sphere we will use volume of sphere formula.

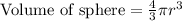`\text{Volume of sphere}=(4)/(3)\pi r^3`, where r represents the radius of sphere.

Upon substituting our given volume in above formula we will get,

`(1)/(48)\pi\text{ m}^3=(4)/(3)\pi r^3`

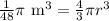
Let us multiply both sides of our equation by 3/4.

`(3)/(4)*(1)/(48)\pi\text{ m}^3=(3)/(4)*(4)/(3)\pi r^3`

`(\pi)/(4* 16)\text{ m}^3=\pi r^3`

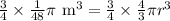
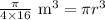
Dividing both sides of our equation by pi we will get,

`(\pi)/(64\pi)\text{ m}^3=(\pi r^3)/(\pi)`

`(1)/(64)\text{ m}^3=r^3`

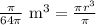
Taking cube root of both sides of our equation we will get,

`\sqrt[3]{(1)/(64)\text{ m}^3}=r`

`\sqrt[3]{(1)/(4^3)\text{ m}^3}=r`

`(1)/(4)\text{ m}=r`

`r=(1)/(4)\text{ m}=0.25\text{ m}`

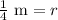
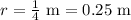
Therefore, the radius of sphere is 0.25 meters.