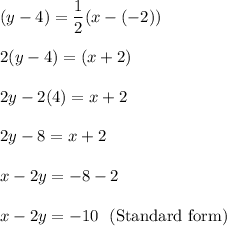Answer:

Explanation:
Write
 in intercept form(
in intercept form(
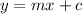 ).
).
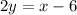

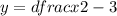
Here , slope of line
 =
=
 (Coefficient of x)
(Coefficient of x)
Also , the slope of two parallel lines are equal.
Equation of line passing through point (a,b) and has slope m is given by :_
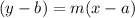
Standard form of equation :
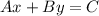 ,where A is positive integer a,d B and C be any integer.
,where A is positive integer a,d B and C be any integer.
Equation of the line parallel to line
 and passing through (-2, 4) will be :-
and passing through (-2, 4) will be :-