Question

A chef plans to mix 100% vinegar with Italian dressing. The Italian dressing contains 16% vinegar. The chef wants to make 210 milliliters of a mixture that contains 48% vinegar. How much vinegar and how much Italian dressing should she use?

Answer 1

Explanation:

80 - Vinegar

130 - Italian Dressing

Answer 2

now, how much vinegar is in the dressing anyway? now, the dressing contains other substances, but just vinegar, we know is 16% in it, therefore, if we use say "y" mL of dressing, how much is 16% of y? well, (16/100) * y, or 0.16y. So that much vinegar will be in that "y" mLs.

now, we're also mixing pure vinegar, how much vinegar is in pure vinegar?

well, is pure vinegar, so is 100% vinegar, so if we use say "x" mL, that'll be (100/100) * x, or 1.00x or just x.

and the mixture we know needs to be 210mLs at 48% vinegar, so that'd be (48/100) * 210 or 100.8 of vinegar in the mixture.

bear in mind that whatever "x" and "y" are, they must yield 210 for the mixture, thus x + y = 210.

and the vinegar quantities, must also yield the mixture requirement, thus x + 0.16y = 100.8.


`\bf \begin{array}{lccclll} &\stackrel{mL}{amount}&\stackrel{vinegar~\%}{quantity}&\stackrel{vinegar~mL}{quantity}\\ &------&------&------\\ \textit{pure vinegar}&x&1.00&1.00x\\ \textit{16\% vinegar dressing}&y&0.16&0.16y\\ ---------&------&------&------\\ mixture&210&0.48&100.8 \end{array}`


`\bf \begin{cases} x+y=210\implies \boxed{y}=210-x\\ x+0.16y=100.8\\ ----------\\ x+0.16\left( \boxed{210-x} \right)=100.8 \end{cases} \\\\\\ x-0.16x+33.6=100.8\implies 0.84x=67.2 \\\\\\ x=\cfrac{67.2}{0.84}\implies x=\stackrel{mL}{80}`

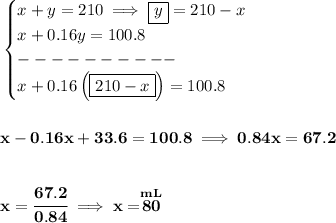
how much will it be of the dressing? well, y = 210 - x.