Question

Consider the function f(x)=cos(0.9x).How much does x have to increase by for 0.9x to increase by 2π?What is the period of f?Consider the function g(x)=sin(5πx).How much does x have to increase by for 5πx to increase by 2π?What is the period of g?

Answer 1

Let Δx be an increase in the variable such that 0.9x increases by 2π. Then:

`\begin{gathered} 0.9(x+\Delta x)-0.9x=2\pi \\ \Rightarrow0.9x+0.9\Delta x-0.9x=2\pi \\ \Rightarrow0.9\Delta x=2\pi \\ \Rightarrow\Delta x=(2\pi)/(0.9) \\ \therefore\Delta x=(20\pi)/(9) \end{gathered}`

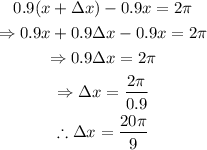
The period of a function f is a quantity T such that for every x, then:

`f(x)=f(x+T)`

The cosine function has a period of 2π over its argument. In this case, we know that:

`f(x)=\cos (0.9x)`

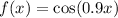
The argument of cosine is 0.9x and we already know that for an increase of 20π/9 in x, there is an increase of 2π in 0.9x. Therefore:

`\begin{gathered} f(x+(20\pi)/(9))=\cos (0.9(x+(20\pi)/(9))) \\ =\cos (0.9x+0.9\cdot(20\pi)/(9)) \\ =\cos (0.9x+2\pi) \\ =\cos (0.9x) \\ =f(x) \end{gathered}`

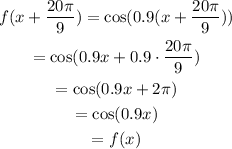
Then, for every x we know that:

`f(x+(20\pi)/(9))=f(x)`

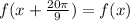
Therefore, the period of f is:

`(20\pi)/(9)`

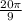
Following a similar process, we can find the period of the function g. Since we know that the period of the sine function is also 2π.

`\begin{gathered} 5\pi\Delta x=2\pi \\ \Rightarrow\Delta x=(2\pi)/(5\pi) \\ \therefore\Delta x=(2)/(5) \end{gathered}`

Therefore, the period of g is:

`(2)/(5)`