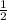What is the constant of proportionality for the relationship shown in the table A.1/2 B.2 C.4 D.8

Question

asked Feb 11, 2018 42.4k views

2 Answers

Yohei · Answer 1 · 2018-02-14T08:34:19+0000

Answer:

Option A is correct

(1)/(2)

Explanation:

Direct proportionality states:

if
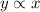
$y \propto x$

then, the equation is in the form of:

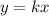y = kx ......[1] where, k is the constant of proportionality.

As per the statement:

Consider any points from the given table:

Let (x, y) = (4, 2)

Substitute these points in [1] we have;

2 = 4k

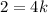
Divide both sides by 4 we have;

(1)/(2) = k

or

k=(1)/(2)

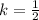
Therefore, the constant of proportionality for the relationship is,

Ido Barash · Answer 2 · 2018-02-16T00:26:58+0000

Answer:

Option A

1/2

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
y/x=k or
y=kx

In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

so

For
x=2, y=1

k=y/x=1/2

For
x=4, y=2

k=2/4=1/2

For
x=6, y=3

k=3/6=1/2

For
x=8, y=4

k=4/8=1/2