The correct option has been marked in the Figure below. A function
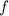 from a set
from a set
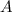 to a set
to a set
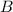 is a relation that assigns to each element
is a relation that assigns to each element
 in the set
in the set
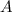 exactly one element
exactly one element
 in the set
in the set
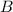 . The set
. The set
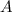 is the domain (also called the set of inputs) of the function and the set
is the domain (also called the set of inputs) of the function and the set
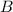 contains the range (also called the set of outputs).
contains the range (also called the set of outputs).
For our correct option we have:
Set A, Domain:
Inputs: -2, 1, 0, 1, 2, 3
Set B, Range:
Outputs: -1, 0, 1, 2, 3
This is a function because this is a relation that assigns to each element
 in the set
in the set
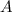 exactly one element
exactly one element
 in the set
in the set
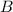 . So, the assignation is as follow:
. So, the assignation is as follow:
- -2 (in x) matches to 0 (in y)
- -1 (in x) matches to 3 (in y)
- 0 (in x) matches to 2 (in y)
- 1 (in x) matches to -1 (in y)
- 2 (in x) matches to 0 (in y)
- 3 (in x) matches to 2 (in y)