Question

AD¯¯¯¯¯ , BD¯¯¯¯¯ , and CD¯¯¯¯¯ are angle bisectors of the sides of △ABC . CF=8 m and CD=17 m.

What is DE ?

Enter your answer in the box.

Answer 1

To solve this you have to use the Pythagorean Theorem.
Which is a²+b²=c²
CF,CD,and DF makes a triangle
Substitute it in
a²+8²=17² Add
a²+64=289 Subtract 64 to get a alone
a²=225 Square root it
a=15

Answer 2

Answer: DE= 15 m

Explanation:

Since, in
`\triangle CDF`,

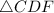After applying, Pythagoras theorem,
`DF^2=CD^2-CF^2=(17)^2-(8)^2=289-64=225`

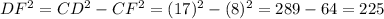
Thus,
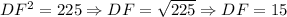`DF^2=225 \Rightarrow DF=√(225) \Rightarrow DF=15` m

Again, in
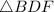`\triangle BDF` and
`\triangle BDE`,

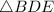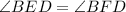`\angle BED= \angle BFD` ( Right angles)

BD=BD ( common edges)

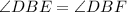`\angle DBE= \angle DBF` (BD makes the angle bisector of angle B.)

Thus, according to AAS condition-
`\triangle BDF\cong \triangle BDE`

So, DE=DF (CPCT)

Therefore, DE=DF=15m⇒DE=15 m