Question

Need help asap!! will rate 5 stars!!

A system of equations is shown below:

n = 3m + 7
n − 2m = 1

What is the solution, in the form (m, n), to the system of equations?

(3, 7)
(1, 8)
(−3, −2)
(−6, −11)


Which statement is true about the solutions for the equation 4y + 6 = −2?

It has infinitely many solutions.
It has two solutions.
It has one solution.
It has no solution.


The system of equations shown below is graphed on a coordinate grid:

3y + x = 4
2y − x = 6

Which statement is true about the coordinates of the point that is the solution to the system of equations?

It is (−2, 2) and lies on both lines.
It is (−5, 3) and lies on both lines.
It is (−5, 3) and does not lie on either line.
It is (−2, 2) and does not lie on either line.


What is the value of z in the equation 2z + 6 = −4?

5
1
−1
−5


Which statement is true for the equation 2x − 2x − 7 = −7?

It has infinitely many solutions.
It has two solutions.
It has one solution.
It has no solution.


The incomplete work of a student to solve an equation is shown below:

Step 1: 4x + 12 = 4
Step 2: ?
Step 3: x = −8 ÷ 4
Step 4: x = −2

What is the missing Step 2?

4x = 8
4x = 16
4x = −16
4x = −8



Which set of steps shows the solution to the equation 2y = −8?

y = −8 − 2; y = 6
y = −8 ÷ (−2); y = 4
y = −8 ÷ 2; y = −4
y = −8 − (−2); y = −6



A system of two equations is shown below:

Equation C: a = 3b + 6
Equation D: a = 7b − 1

What value of a can be substituted into equation D to solve the system of equations?

3b
7b
3b + 6
7b − 1

Answer 1

1. (-6, -11)

2. It has one solution

3. It is (−2, 2) and lies on both lines

4.
`-5`

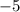
5. It has infinitely many solutions.

6.
`4x=-8`

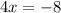
7. y = −8 ÷ 2; y = −4

8. 3b + 6

Explanation:

Question 1:

Substituting equation 1 into equation 2 and solving for
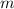`m` gives us:

`n-2m=1\\(3m+7)-2m=1\\m+7=1\\m=1-7\\m=-6`

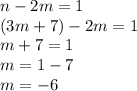
Plugging this value into equation 1 gives us
`n`, so we have:

`n=3m+7\\n=3(-6)+7\\n=-18+7\\n=-11`

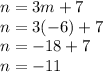
Hence, the solution, in the form (m, n), to the system of equations is (-6,-11).

Question 2:

Solving the equation for
`y` gives us:

`4y+6=-2\\4y=-2-6\\4y=-8\\y=(-8)/(4)=-2`

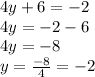
As we can see, there is only one solution.

Question 3:

We can add the both equations so
`x` cancels out and then we can solve for
`y`:

`(3y+x=4)\\+(2y-x=6)\\---------\\5y=10\\y=(10)/(5)=2`

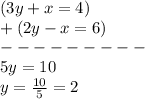
Substituting this value of
`y` into any equation above (let's use equation 1) will give us
`x`:

`3y+x=4\\3(2)+x=4\\6+x=4\\x=4-6\\x=-2`

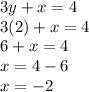
So the intersection point (or solution) (-2, 2) lies on both the lines.

Question 4:

Let's do some algebra and figure out the value of
`z`:

`2z+6=-4\\2z=-4-6\\2z=-10\\z=(-10)/(2)=-5`

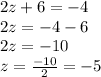
`z` is -5

Question 5:

Reducing the equation gives us:

`2x-2x-7=-7\\0-7=-7\\-7=-7`

We can plug in ANY VALUE into
`x` and make this equation true. So there are INFINITELY MANY SOLUTIONS.

Question 6:

Step 2 of the solution should be taking 12 to the other side so that variable is on one side and all the numbers to the other. So 2nd step would be:

`4x+12=4\\4x=4-12\\4x=-8`

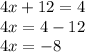
Rest of the steps follow. So, 2nd step would be
`4x=-8`.

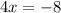Question 7:

The next step to solving this equation would be to DIVIDE -8 by 2 since 2 is multiplied with
`y`.

`2y=-8\\y=(-8)/(2)=-4`

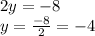
Third answer choice is right.

Question 8:

We can substitute the value of
`a` given in Equation C into Equation D to solve the system of equations.

The value of
`a` in Equation C is given as
`a=3b+6`

Third answer choice is right.