The general equation of line is :
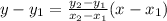
The equation of the function g(x) is:
Consider any two coordinates : (-3,0) & (0,3) So, the equation is:
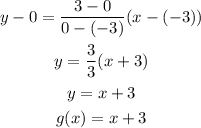
The equation of the function f(x) is:
Consider any two coordinates: (-1,0) & (0,1)
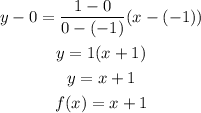
Since, h(x) = f(x)/g(x)
So, the funstion h(x) is express as:
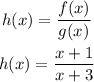
a) Vertical intercept of h
Substitute x =0 in h(x)
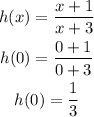
b) Determine the roots of h(x)
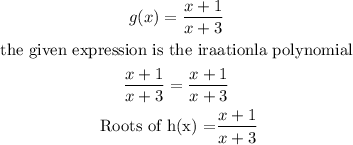
c) Vertical asymptote : Vertical asymptotes are vertical lines which correspond to the zeroes of the denominator of a rational function
So,
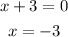
The vertical assymptote : x =-3
D) Horizontal assymptote : x - 3
bAnswer: x -3
Answer:
a)h(0)=1/3
b) h(x)=(x+1)/(x+3)
c) x = -3
Hroizontal Assymotote : y =1/3