Question

Which of the following equations have only one solution? Select all correct answers. 4x 2 + 4x = 0 x 2 + 6x + 9 = 0 9x 2 - 25 = 0 5x 2 + 20x + 20 = 0 x 2 - x - 6 = 0

Answer 1

The equations which have only one solution are: x²+6x+9=0 and 5x²+20x+20=0,

Answer 2

2nd and 4th equation will have only one solution.

Explanation:

1). 4x² + 4x = 0

4x(x + 1) = 0

x = 0

or (x + 1) = 0 ⇒ x = -1

2). x² + 6x + 9 = 0

(x + 3)² = 0

(x + 3) = 0

x = -3

3). 9x² - 25 = 0

9x² = 25

x² =
`(25)/(9)`

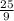
x = ±
`\sqrt{(25)/(9) }`

x = ±
`(5)/(3)`

4). 5x² + 20x + 20 = 0

5(x² + 4x + 4) = 0

(x + 2)²= 0

x + 2 = 0

x = -2

5). x² - x - 6 = 0

x² - 3x + 2x - 6 = 0

x(x - 3) + 2(x - 3) = 0

(x + 2)(x - 3) = 0

x = -2 or x = 3

Therefore, 2nd and 4th equations have only one solution.