Question

What are the coordinates of the endpoints of the midsegment for △RST that is parallel TS¯¯¯¯¯ ?

Enter your answers in the boxes.

Answer 1

All you have to do is use the Midpoint formula
`(x+x)/(2) , (y+y)/(2)` Plug in Rs and RT points to get (1,3) and (4,3).
Hope this helps if u have any questions just pm me :).

Answer 2

The coordinates of the endpoints of the mid-segment for ΔRST that is parallel TS are (4, 3) and (1, 3)

Solution-

The coordinates of the vertices are,

T = (2, 0)

R = (0, 6)

S = (8, 0)

Triangle Midpoint Theorem-

The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side.

So, the line joining the midpoints of TS and RS is always parallel to TS.

Midpoint formula,

`((x_1+x_2)/(2),\ (y_1+y_2)/(2))`

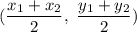
Midpoint of RS is

`=((0+8)/(2),\ (6+0)/(2))`

`=(4,\ 3)`

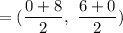
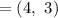
Midpoint of RT is

`=((2+0)/(2),\ (0+6)/(2))`

`=(1,\ 3)`

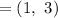
Therefore, the coordinates of the endpoints of the mid-segment for ΔRST that is parallel TS are (4, 3) and (1, 3)