Question

If you're good at basic geometry , help please!these two problems are due today at 12 am

Answer 1

Parallel and transversal lines

Angles

We know that the angles

m∠XWZ = m∠XMN

m∠XYZ = m∠MNZ

The following pair of angles form a straight line (called supplementary angles):

m∠MNZ and m∠MNY

since the addition of supplementary angles is 180°, then

m∠MNZ + m∠MNY = 180°

Having this information we are going to complete the right cuadrilateral's angles:

Assuming that this is an isosceles trapezoid:

we have that the angles

m∠XMN and m∠MNY are equal, then

2x - 7 = 63

We want to find x from the equation:

2x - 7 = 63

↓ adding 7 both sides

2x = 63 + 7

2x = 70

↓ dividing both sides by 2

2x/2 = 70/2

x = 35°

Answer: x = 35°

Sides

We know that the lenght of the middle line is given by

`\frac{\text{big segment + small segment}}{2}=Segment\text{ of the middle}`

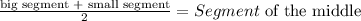
Then

`(WZ+XY)/(2)=MN`

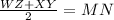
replacing them with the given information:

`((6x+11)+(4x-1))/(2)=60`

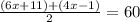
Now, we can find x

`\begin{gathered} (6x+11+4x-1)/(2)=60 \\ (10x+10)/(2)=60 \\ 10x+10=60\cdot2 \\ 10x+10=120 \\ 10x=120-10 \\ 10x=110 \\ x=(110)/(11) \\ x=10 \end{gathered}`

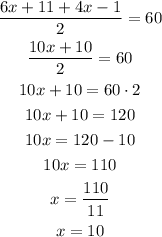
Answer: x = 10