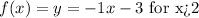Question

I am looking to find the piecewise functions represented by this graph. I know some of the information this graph is providing, but not all of it.

Answer 1

You need to find the functions for each part of the graph.

All 3 parts are linear functions, given by the general form

`y=mx+b\begin{cases}m=\text{slope} \\ b=y-\text{intercept}\end{cases}`

You can find the slope as follows:

`m=(y2-y1)/(x2-x1)`

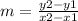
Let's evaluate a pair of points in each part of the graph to find the correspondent slope:

Part 1. Point 1 = (-2, 0) and Point 2= (0, 2)

`m1=(2-0)/(0-(-2))=(2)/(2)=1`

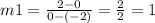
The y-intercept is the point where it crosses the y-axis, for the first part of the graph you can see it at y=2, then b=2

The function of this part is then:

`f(x)=y=1\cdot x+2\text{ for x}\leq0`

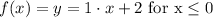
Part 2. Point 1 = (0, 1) and Point 2= (1, 1.4)

`m2=(1.4-1)/(1-0)=(0.4)/(1)=0.4`

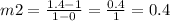
The y-intercept is at b=1, then the function for the second part is:

In this case, we can't see the point where the function crosses the y-axis, thus we need to evaluate the general form of the linear equation, replacing the slope and one of the known points

`\begin{gathered} y=mx+b\text{ replace the values} \\ -6=-1\cdot3+b\text{ add +3 to both sides} \\ -6+3=-3+3+b \\ -3=b\text{ reorder the terms} \\ b=-3\text{ this is the y-intercept for the third part of the function} \end{gathered}`

The function for the third part is:

`f(x)=y=-1x-3\text{ for x>2}`