Question

(1 point) consider the function f(t)=⎧⎩⎨⎪⎪⎪⎪0,−5,−6,6,t<00≤t<11≤t<7t≥7;f(t)={0,t<0−5,0≤t<1−6,1≤t<76,t≥7; 1. write the function in terms of unit step function

Answer 1

`f(t)=\begin{cases}0&\text{for }t<0\\-5&\text{for }0\le t<1\\-6&\text{for }1\le t<7\\6&\text{for }t\ge7\end{cases}`

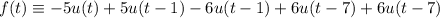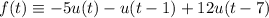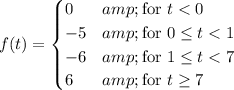
Recall that


`u(t)=\begin{cases}0&\text{for }t<0\\1&\text{for }t\ge0\end{cases}`

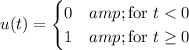
Take it one piece at a time. For
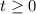
`t\ge0`, we can scale
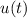
`u(t)` by -5:


`-5u(t)=\begin{cases}0&\text{for }t<0\\-5&\text{for }t\ge0\end{cases}`

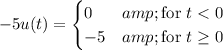
If we shift the argument by 1 and scale by -5, we have


`-5u(t-1)=\begin{cases}0&\text{for }t<1\\-5&\text{for }t\ge1\end{cases}`

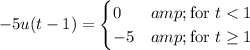
so if we subtract this from
`-5u(t)`, we'll end up with


`-5u(t)+5u(t-1)=\begin{cases}0&\text{for }t<0\text{ and }t\ge1\\-5&\text{for }0\le t<1\end{cases}`

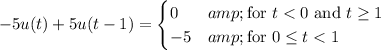
For the next piece, we can add another scaled and shifted step like


`-6u(t-1)+6u(t-7)=\begin{cases}0&\text{for }t<1\text{ and }t\ge7\\-6&\text{for }1\le t<7\end{cases}`

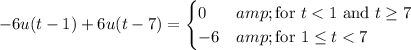
so that


`-5u(t)+5u(t-1)-6u(t-1)+6u(t-7)=\begin{cases}0&\text{for }t<0\text{ and }t\ge7\\-5&\text{for }0\le t<1\\-6&\text{for }1\le t<7\end{cases}`

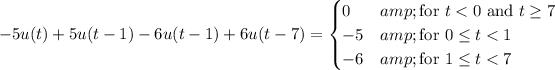
For the last piece, we add one more term:


`6u(t-7)=\begin{cases}0&\text{for }t<7\\6&\text{for }t\ge7\end{cases}`

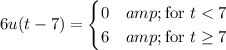
and so putting everything together, we get
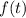
`f(t)`:


`f(t)\equiv-5u(t)+5u(t-1)-6u(t-1)+6u(t-7)+6u(t-7)`

`f(t)\equiv-5u(t)-u(t-1)+12u(t-7)`